چهل و یکمین عدد مرسن شناخته شد
![]()

پس از گذشت کمتر از شش ماه از اکتشاف چهلمین عدد اول مرسن عدد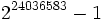
با 7,235,733 رقم نه تنها به عنوان بزرگترین عدد اول مرسن شناخته شده بلکه به عنوان بزرگترین عدد اولی که تا کنون کشف شده است شناخته شد. طبق گزارشی که در سایت "کشف اینترنتی اعداد اول مرسن" (GIMPS) ارائه شد این عدد از الگوریتم "لوکاس- لمر" با موفقیت عبور کرده و در نتیجه عددی اول می باشد.



.gif)
.gif)











